Routine verification measures for radar-based precipitation estimates#
[1]:
import wradlib as wrl
import os
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
try:
get_ipython().run_line_magic("matplotlib inline")
except:
plt.ion()
Extract bin values from a polar radar data set at rain gage locations#
Read polar data set#
[2]:
filename = wrl.util.get_wradlib_data_file("misc/polar_R_tur.gz")
data = np.loadtxt(filename)
Downloading file 'misc/polar_R_tur.gz' from 'https://github.com/wradlib/wradlib-data/raw/pooch/data/misc/polar_R_tur.gz' to '/home/runner/work/wradlib/wradlib/wradlib-data'.
Define site coordinates (lon/lat) and polar coordinate system#
[3]:
r = np.arange(1, 129)
az = np.linspace(0, 360, 361)[0:-1]
site = (9.7839, 48.5861, 0)
Make up two rain gauge locations (say we want to work in Gaus Krueger zone 3)#
[4]:
# Define the projection via epsg-code
crs = wrl.georef.epsg_to_osr(31467)
# Coordinates of the rain gages in Gauss-Krueger 3 coordinates
x, y = np.array([3557880, 3557890]), np.array([5383379, 5383375])
Now extract the radar values at those bins that are closest to our rain gauges#
For this purppose, we use the PolarNeighbours class from wraldib’s verify module. Here, we extract the 9 nearest bins…
[5]:
polarneighbs = wrl.verify.PolarNeighbours(r, az, site, crs, x, y, nnear=9)
radar_at_gages = polarneighbs.extract(data)
print("Radar values at rain gauge #1: %r" % radar_at_gages[0].tolist())
print("Radar values at rain gauge #2: %r" % radar_at_gages[1].tolist())
Radar values at rain gauge #1: [0.01, 0.02, 0.01, 0.01, 0.02, 0.05, 0.01, 0.01, 0.01]
Radar values at rain gauge #2: [0.2, 0.06, 0.15, 0.69, 0.06, 0.26, 0.05, 0.99, 0.32]
Retrieve the bin coordinates (all of them or those at the rain gauges)#
[6]:
binx, biny = polarneighbs.get_bincoords()
binx_nn, biny_nn = polarneighbs.get_bincoords_at_points()
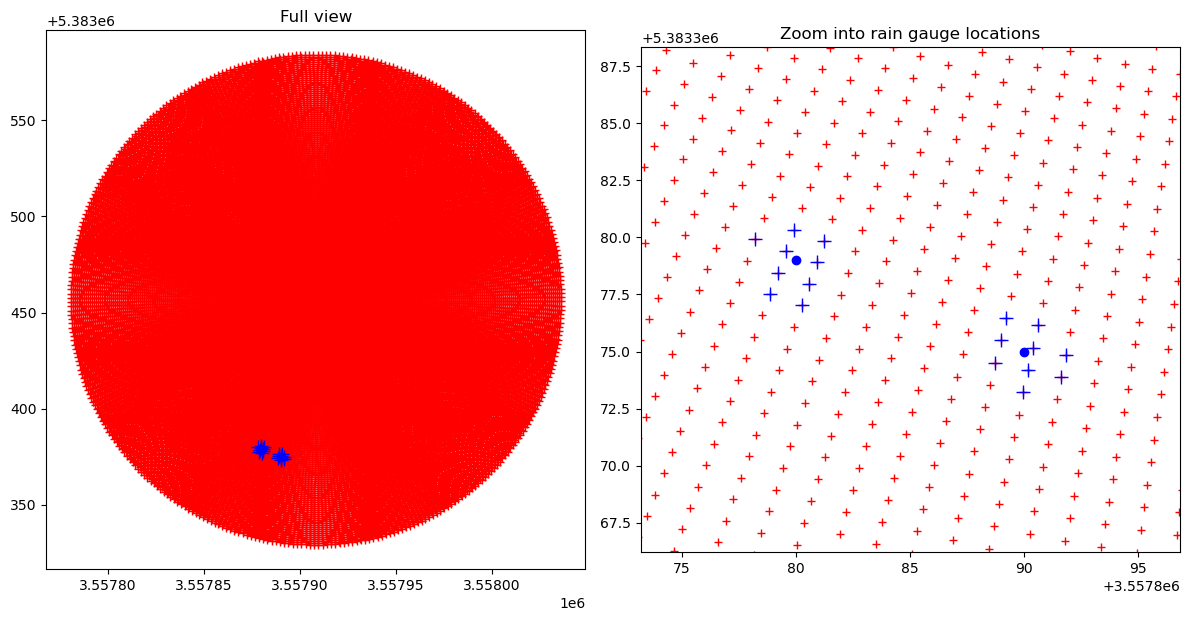
Plot the entire radar domain and zoom into the surrounding of the rain gauge locations#
[7]:
fig = plt.figure(figsize=(12, 12))
ax = fig.add_subplot(121)
ax.plot(binx, biny, "r+")
ax.plot(binx_nn, biny_nn, "b+", markersize=10)
ax.plot(x, y, "bo")
ax.axis("tight")
ax.set_aspect("equal")
plt.title("Full view")
ax = fig.add_subplot(122)
ax.plot(binx, biny, "r+")
ax.plot(binx_nn, biny_nn, "b+", markersize=10)
ax.plot(x, y, "bo")
plt.xlim(binx_nn.min() - 5, binx_nn.max() + 5)
plt.ylim(biny_nn.min() - 7, biny_nn.max() + 8)
ax.set_aspect("equal")
txt = plt.title("Zoom into rain gauge locations")
plt.tight_layout()
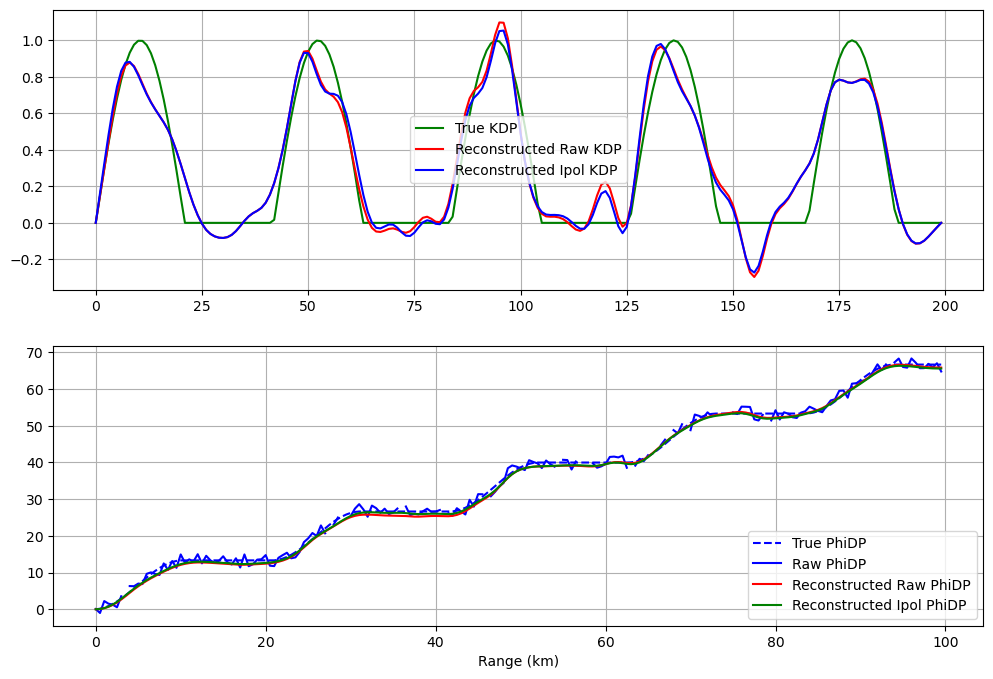
Create a verification report#
In this example, we make up a true Kdp profile and verify our reconstructed Kdp.
Create synthetic data and reconstruct KDP#
[8]:
# Synthetic truth
dr = 0.5
r = np.arange(0, 100, dr)
kdp_true = np.sin(0.3 * r)
kdp_true[kdp_true < 0] = 0.0
phidp_true = np.cumsum(kdp_true) * 2 * dr
# Synthetic observation of PhiDP with a random noise and gaps
np.random.seed(1319622840)
phidp_raw = phidp_true + np.random.uniform(-2, 2, len(phidp_true))
gaps = np.random.uniform(0, len(r), 20).astype("int")
phidp_raw[gaps] = np.nan
# linearly interpolate nan
nans = np.isnan(phidp_raw)
phidp_ipol = phidp_raw.copy()
phidp_ipol[nans] = np.interp(r[nans], r[~nans], phidp_raw[~nans])
# Reconstruct PhiDP and KDP
phidp_rawre, kdp_rawre = wrl.dp.phidp_kdp_vulpiani(phidp_raw, dr=dr)
phidp_ipre, kdp_ipre = wrl.dp.phidp_kdp_vulpiani(phidp_ipol, dr=dr)
# Plot results
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(211)
plt.plot(kdp_true, "g-", label="True KDP")
plt.plot(kdp_rawre, "r-", label="Reconstructed Raw KDP")
plt.plot(kdp_ipre, "b-", label="Reconstructed Ipol KDP")
plt.grid()
lg = plt.legend()
ax = fig.add_subplot(212)
plt.plot(r, phidp_true, "b--", label="True PhiDP")
plt.plot(r, np.ma.masked_invalid(phidp_raw), "b-", label="Raw PhiDP")
plt.plot(r, phidp_rawre, "r-", label="Reconstructed Raw PhiDP")
plt.plot(r, phidp_ipre, "g-", label="Reconstructed Ipol PhiDP")
plt.grid()
lg = plt.legend(loc="lower right")
txt = plt.xlabel("Range (km)")
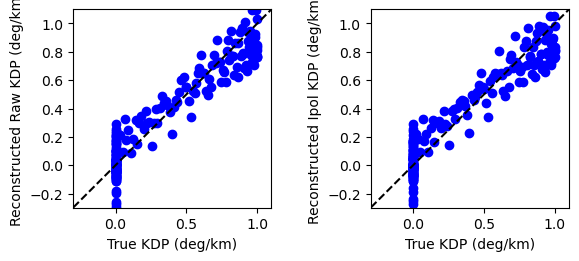
Create verification report#
[9]:
metrics_raw = wrl.verify.ErrorMetrics(kdp_true, kdp_rawre)
metrics_raw.pprint()
metrics_ip = wrl.verify.ErrorMetrics(kdp_true, kdp_ipre)
metrics_ip.pprint()
plt.subplots_adjust(wspace=0.5)
ax = plt.subplot(121, aspect=1.0)
ax.plot(metrics_raw.obs, metrics_raw.est, "bo")
ax.plot([-1, 2], [-1, 2], "k--")
plt.xlim(-0.3, 1.1)
plt.ylim(-0.3, 1.1)
xlabel = ax.set_xlabel("True KDP (deg/km)")
ylabel = ax.set_ylabel("Reconstructed Raw KDP (deg/km)")
ax = plt.subplot(122, aspect=1.0)
ax.plot(metrics_ip.obs, metrics_ip.est, "bo")
ax.plot([-1, 2], [-1, 2], "k--")
plt.xlim(-0.3, 1.1)
plt.ylim(-0.3, 1.1)
xlabel = ax.set_xlabel("True KDP (deg/km)")
ylabel = ax.set_ylabel("Reconstructed Ipol KDP (deg/km)")
{'corr': 0.95,
'mas': 0.1,
'meanerr': -0.0,
'mse': 0.01,
'nash': 0.93,
'pbias': -0.0,
'r2': 0.9,
'ratio': nan,
'rmse': 0.1,
'spearman': 0.92,
'sse': 2.96}
{'corr': 0.95,
'mas': 0.1,
'meanerr': -0.01,
'mse': 0.01,
'nash': 0.93,
'pbias': -3.0,
'r2': 0.91,
'ratio': nan,
'rmse': 0.1,
'spearman': 0.92,
'sse': 2.91}